DOMINO SOLITAIRE
The numerical pattern on the diagram is nothing but 28 domino tiles, creating a 7 x 8 rectangle consisting of 56 squares. Every tile occupies two squares. The borders of the tiles are not shown.

Your job is to restore the borders, i.e., to figure out which adjacent squares form each domino, in order to produce a complete set of dominoes from 0:0 to 6:6.
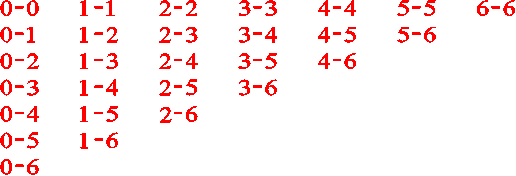
When solving this problem it helps to make a list of tile combinations, crossing them out as you find them in the diagram.
First, tile 0:1 must occupy squares B2 and B3 because nowhere else in the diagram are 0 and 1 side by side. The same can be said of tiles 2:4 and 5:6. They must occupy squares C3 and D3 and E1 and E2.
Since the tiles in the squares C1, C2, D1, and D2 must combine to make two dominoes somehow, B1 must be part of the same tile as A1 – 5:5.
Similarly, 3:3 must be tile A2-A3.
Since the 3:3 combination has already been used in A2-A3, it cannot appear again in C2-D2. Therefore, C1 and C2 go together, as do D1 and D2, forming 0:3 and 2:3, respectively.
Look at the square E3. It may be a part of the tile E3-F3 (0:4) or E3-E4 (0:3). Since 0:3 has been identified, it must be 0:4, on squares E3-F3.
Just as we determined the position of 5:5, tile 4:4 must be on squares G3-G4, tile 3:4 on squares F1-G1, and tile 4:5 on squares F2, G2. Knowing the position of 3:4 determines the position of tile 1:4 on F4-F5. Therefore tile G5-G6 must be 1:6.
Using this reasoning determines the position of the tiles 1:3 (E6-F6), 3:5 (D4-E4), and 1:5 (D5-E5). The position of the tile 1:6 was determined earlier. Hence tile 1:2 is on squares D6-D7 and tile 2:5 on squares C8-D8. After that we may find a place for the tile 2:6 (F7-G7), 0:5 (F8-G8) and 0:6 (E7-E8). This allows us to find the positions of the tile 0:2 (A4-B4) and 2:2 (C4-C5).
There are only five tiles left: 0:0, 1:1, 3:6, 4:6, and 6:6. 0:0 and 1:1 must be at A7-A8 and B5-B6, respectively. This determines the position of 6:6 (A5-A6), 3:6 (C6-C7), and 4:6 (B7-B8).
The solution is complete.
First, tile 0:1 must occupy squares B2 and B3 because nowhere else in the diagram are 0 and 1 side by side. The same can be said of tiles 2:4 and 5:6. They must occupy squares C3 and D3 and E1 and E2.
Since the tiles in the squares C1, C2, D1, and D2 must combine to make two dominoes somehow, B1 must be part of the same tile as A1 – 5:5.
Similarly, 3:3 must be tile A2-A3.
Since the 3:3 combination has already been used in A2-A3, it cannot appear again in C2-D2. Therefore, C1 and C2 go together, as do D1 and D2, forming 0:3 and 2:3, respectively.
Look at the square E3. It may be a part of the tile E3-F3 (0:4) or E3-E4 (0:3). Since 0:3 has been identified, it must be 0:4, on squares E3-F3.
Just as we determined the position of 5:5, tile 4:4 must be on squares G3-G4, tile 3:4 on squares F1-G1, and tile 4:5 on squares F2, G2. Knowing the position of 3:4 determines the position of tile 1:4 on F4-F5. Therefore tile G5-G6 must be 1:6.
Using this reasoning determines the position of the tiles 1:3 (E6-F6), 3:5 (D4-E4), and 1:5 (D5-E5). The position of the tile 1:6 was determined earlier. Hence tile 1:2 is on squares D6-D7 and tile 2:5 on squares C8-D8. After that we may find a place for the tile 2:6 (F7-G7), 0:5 (F8-G8) and 0:6 (E7-E8). This allows us to find the positions of the tile 0:2 (A4-B4) and 2:2 (C4-C5).
There are only five tiles left: 0:0, 1:1, 3:6, 4:6, and 6:6. 0:0 and 1:1 must be at A7-A8 and B5-B6, respectively. This determines the position of 6:6 (A5-A6), 3:6 (C6-C7), and 4:6 (B7-B8).
The solution is complete.

Find solutions for the following puzzles: